Coco Sketch
Space Saving算法
- 如果元素在集合中,将其对应的计数器自增;
- 如果元素不在集合中且集合未满,就将元素加入集合,计数器设为1;
- 如果元素不在集合中且集合已满,将集合内计数器值最小的元素移除,将新元素插入到它的位置,并且在原计数值的基础上自增。
这样操作的好处是,所有计数器的和一定等于数据流的总元素数m(因为不需要做减法,只需要自增),且那些没有被移除过的元素的计数值是准确的。容易分析得出:
集合中最小的计数值min一定不会大于m / k = εm,同时能够保证找出所有频率大于εm的元素;
元素出现频率的估计误差同样在εm的范围内,不过会偏高;
Space Saving算法也有假阳性的问题,特别是在非频繁项集中位于流的末尾时。
Unbiased Space Saving算法
在替换更新的时候必然产生有偏误差,可以直观的看出当计数器值越大,他变更的惩罚代价越大。因此我们更改一下策略,我们以1/(原值+1)的概率把它替换为新元素,否则保持不变
CocoSketch
提出了任意部分键查询方法
现有方案的局限性:
One single-key sketch per key:为每个键创建单独sketch 显然可以发现很可能需要sketch个数非常多,而占用过多内存无法合理的实现
Full-key sketch with post recovery: 先按全键建立sketch并查询时候进行统计,但按照如下两个方式都不理想:1)直接查询所有可能的键值对应的流,但显然查询范围过大,无法实现;2)只统计sketch显式记录的对应全键,这样误差积累会产生较大误差
Subset sum estimation: 如USS算法,但由于其更新延时较高,仍有局限性,因此提出了cocosketch
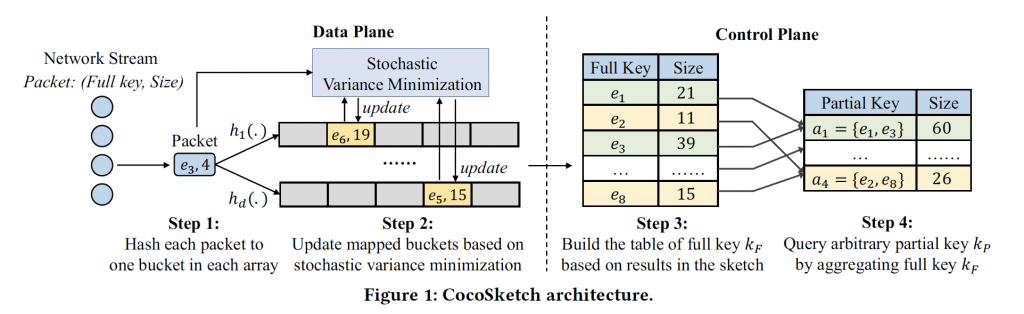
Basic CocoSketch
将每个传进来的packet 定义为(e,w),e代表一个特定的 full key,w是它的增量大小。如何将packet(e,w)插入到sketch?首先根据d个数组的哈希函数,分别将流键 e 映射到 d个array的bucket中,再根据 随机方差最小化 来决定更新哪个bucket的值。这里有两种情况:
(1)如果 e 匹配到 d 个bucket中的任意一个,直接以增量w增加bucket的值,然后返回。
(2)如果 e 匹配不到,则找到其中value值最小的bucket(假设是,其中代表对其做哈希散列),给它的value值增加 w ,然后以概率 用新来的键 e 替换掉原来的键。如果有多个bucket的value值一样且最小,随机选一个更新。
Hardware-friendly insertion
消除循环依赖,提高并行度,提升硬件资源的利用率
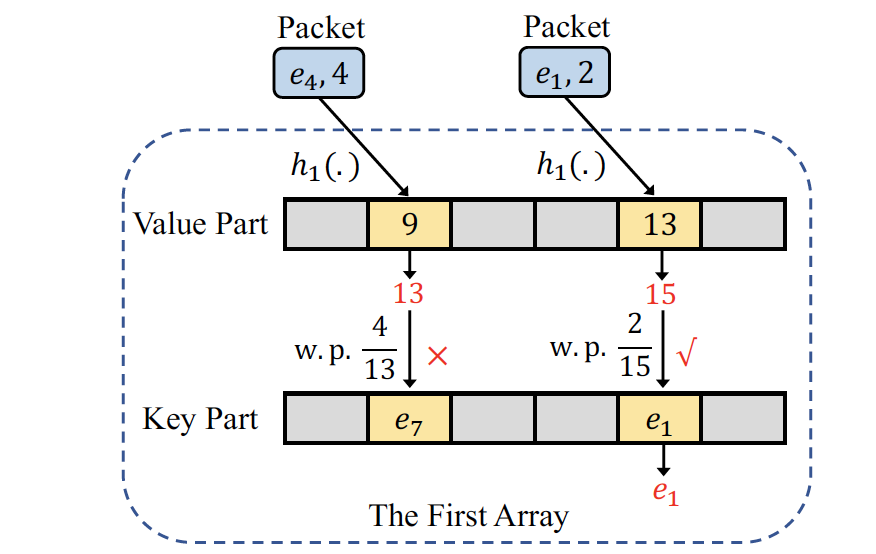
我们将原先的更新修改为对于每个bucket都进行更新,而不是选择最小的,这样我们相当于独立进行了d次的更新操作,同时我们可以将val和key分离,这样更提高了并行度
查询操作:
我们首先通过查询记录的全键流的sketch,构建一个包含两列(全键,大小)的表(即,每个记录流的估计大小的表)。
在 硬件友好的CocoSketch 中,由于一个流可能出现在多个array中,因此我们将以不同array中的中值估计大小作为其最终估计大小。

Hineven
:吸溜吸溜: