bzoj 2508: 简单题 — 数学
Contents
2508: 简单题
Time Limit: 10 Sec Memory Limit: 512 MB Sec Special Judge
Description
求一个点使得它到平面上所有直线距离平方和最小。
你需要实现以下3种操作:
1. 平面上加入一条直线;
2. 删除一条已加入的直线;
3. 求一个点到平面上所有直线距离平方和最小,你需要输出这个最小值。
Input
第1行包含一个整数N,表示了操作数目。接下来N行操作属于下列3种格式之一:
Output
输出行数等于查询操作的次数,每行输出每次查询操作所要求的最小值,保留两位小数。
Sample Input
10
0 0.0 0.0 1.0 0.0
2
0 0 1 1 1
2
0 0 2 1 2
2
1 2
2
1 3
2
0 0.0 0.0 1.0 0.0
2
0 0 1 1 1
2
0 0 2 1 2
2
1 2
2
1 3
2
Sample Output
0.00
0.50
2.00
2.00
0.00【数据规模与约定】
对于10%的数据,N ≤ 25;
对于50%的数据,N ≤ 1000;
对于50%的数据,查询操作不超过10次;
对于70%的数据,N ≤ 20000;
对于100%的数据,N ≤ 120000。
0.50
2.00
2.00
0.00【数据规模与约定】
对于10%的数据,N ≤ 25;
对于50%的数据,N ≤ 1000;
对于50%的数据,查询操作不超过10次;
对于70%的数据,N ≤ 20000;
对于100%的数据,N ≤ 120000。
HINT
一个点到直线Ax+By+C=0 的距离的平方公式是
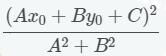
所以我们就可以展开化简成![]()
那么,怎么求他的最值
对于一个正常函数,求最值可求导,导数为0 时就是最值
那么对于一个多变量的函数,我们可以分别对于每一个变量求 (偏)导,得到的解就是最值所在的位置
关于偏导具体可以看一下维基或者百度百科
然后就求一下偏导算一下就好了,剩下就是细节问题了
#include<map>
#include<cmath>
#include<queue>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
#define inf 1000000007
#define ll long long
#define N 120010
#define db double
struct qaz{db a,b,c;}a[N];
int n,tot,ji;
db x,y,xx,yy;
db A,B,C,D,E,F;
void ins()
{
int p=++tot;ji++;
a[p].a=y-yy;a[p].b=xx-x;a[p].c=y*(x-xx)-x*(y-yy);
db tp=(a[p].a*a[p].a+a[p].b*a[p].b);
A+=a[p].a*a[p].a/tp;B+=a[p].b*a[p].b/tp;
C+=2*a[p].a*a[p].b/tp;D+=2*a[p].a*a[p].c/tp;
E+=2*a[p].b*a[p].c/tp;F+=a[p].c*a[p].c/tp;
}
void del(int p)
{
ji--;db tp=(a[p].a*a[p].a+a[p].b*a[p].b);
A-=a[p].a*a[p].a/tp;B-=a[p].b*a[p].b/tp;
C-=2*a[p].a*a[p].b/tp;D-=2*a[p].a*a[p].c/tp;
E-=2*a[p].b*a[p].c/tp;F-=a[p].c*a[p].c/tp;
}
db ans,f[3][4];
#define eps 1e-5
void sol()
{
f[1][1]=2*A;f[1][2]=C;f[1][3]=-D;
f[2][1]=C;f[2][2]=2*B;f[2][3]=-E;
db tx,ty,tt;
if(abs(f[1][1])<eps)
{
if(abs(f[1][2])<eps) tx=0,ty=f[2][3]/f[2][2];
else ty=f[1][3]/f[1][2],tx=(f[2][3]-f[2][2]*ty)/f[2][1];
}
else if(abs(f[2][2])<eps)
{
if(abs(f[2][1])<eps) ty=0,tx=f[1][3]/f[1][1];
else tx=f[2][3]/f[2][1],ty=(f[1][3]-f[1][1]*tx)/f[1][2];
}
else
{
tt=f[2][1]/f[1][1];f[2][1]=0;
f[2][2]-=tt*f[1][2];f[2][3]-=tt*f[1][3];
ty=(abs(f[2][2])<eps)?0:f[2][3]/f[2][2];
tx=(abs(f[1][1])<eps)?0:(f[1][3]-f[1][2]*ty)/f[1][1];
}
ans=abs(A*tx*tx+B*ty*ty+C*tx*ty+D*tx+E*ty+F);
if(ans<eps) puts("0.00");
else printf("%.2lf\n",ans);
}
int main()
{
scanf("%d",&n);
int op,p;
while(n--)
{
scanf("%d",&op);
if(!op)
{
scanf("%lf%lf%lf%lf",&x,&y,&xx,&yy);
ins();
}
else if(op==1)
{
scanf("%d",&p);
del(p);
}
else
{
if(!ji){puts("0.00");continue;}
sol();
}
}
return 0;
}

发表评论